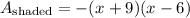The given figure is a rectangle.
Recall that the area of a rectangle is given by

Where L is the length and W is the width of the rectangle.
The area of the shaded region can be obtained by subtracting the area of the inside region from the outside region.
The area of the outside region is

The area of the inside region is

So, the area of the shaded region is
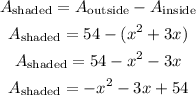
Finally, let us factor out the expression
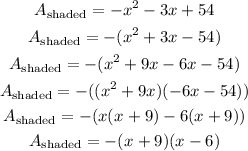
Therefore, the expression in factored form for the shaded area is