Answer: Choice C
============================================================
Step-by-step explanation:
The curly braces tell us we're dealing with a set of values.
The notation
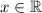 means "x is in the set of real numbers". In other words, it says "x is a real number".
means "x is in the set of real numbers". In other words, it says "x is a real number".
Writing
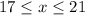 tells the reader that x is between 17 and 21, including both endpoints.
tells the reader that x is between 17 and 21, including both endpoints.
Put everything together and
 means "we have a set of real numbers x that are between 17 and 21, inclusive".
means "we have a set of real numbers x that are between 17 and 21, inclusive".
-------------------------------
Extra info:
- Choice A can be ruled out because there isn't any number that's both smaller than 17 and also larger than 21 at the same time. The set described for choice A simplifies to the empty set.
- Choice B is ruled out because this is only talking about integers between 17 and 21; instead of real numbers. A number like 17.5 is left out when we want to include it.
- Choice D can be ruled out because the endpoints x = 17 and x = 21 are left out (but we want to include them). Also, there's no mention if x is a real number or not.