Question

Do you know how teach me how to write interval notation?

Answer 1

We have the following function

`f(x)=\sqrt[]{x+2}`

A) Domain in interval notation

First, we must remember that the domain of a function is the set of inputs or argument values for which the function is real and defined.

Since we have a root in our function, we must make sure that the radicand is greater than or equal to 0. This is done so that the function is real and defined.

So to find the domain, we must do equality and solve for x, this way we find the limit value at which the function is not definite and real.

`\begin{gathered} x+2=0 \\ x=-2 \end{gathered}`

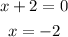
We already have the value of x at which the function ceases to be defined so we find the negative values of the root, in conclusion, the solution is:

`x\ge-2`

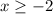
In interval notation:

`\lbrack-2,\infty)`

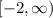
B) Complete the table

`\begin{gathered} f(23)=5 \\ f(47)=7 \\ f(98)=10 \end{gathered}`

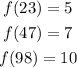
In conclusion:

When x=23 f(X)=5

When x=47 f(X)=7

When x=98 f(X)=10

C) Graph the results

To solve this, we take the values of "x" mentioned to us as a coordinate in "x" and the result as the corresponding coordinate in "y".

Therefore what we must do, is to put the coordinates mentioned in the graph, the coordinates would be as follows:

`\begin{gathered} (23,5) \\ (47,7) \\ (98,10) \end{gathered}`

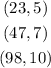
The graph should look something similar to the above image.