Given:
The length of a rectangle is 7 inches more than twice the width, this can be expressed by:

Where:
l = length
w = width
And the area is 22 square inches, which is given by:

Then, substitute the expressions in the area:
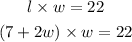
And solve for w:
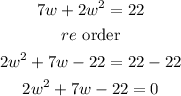
We obtain a quadratic equation, so we solve using the general formula for these equations:
a = 2
b = 7
c = -22
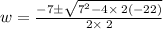
Simplify:
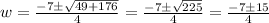
The solutions are:
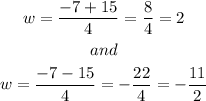
Since a length can't be negative, then the answer is w = 2.
Answer: 2 inches