Question

At a County fair there is a spinner game with 12 sectors: 2 red sectors, 2 green sectors, 2 blue sectors, and 6 yellow sectors. If the spinner lands on a red sector, the player wins 2 tokens. If the spinner lands on a green sector, the player wins 2 tokens. If the spinner lands on a blue sector, the player wins 2 tokens. If the spinner lands on a yellow sector, the player loses 3 tokens. Is this game fair for the player and how much will the player win or lose on an average over time?

A) County fair games are never fair.
B) The expected value is zero, and the game is fair. So the player will break even for a single spin over time.
C) The expected values is 1 2 , and the game is fair. The player will win about 0.55 tokens on a single spin over time.
D) The expected value is -0.5, and the game is not fair. So the player will lose about 0.5 tokens for a single spin over time.

Answer 1

D, theres a 50 50 chance to win or loose, but  if you loose 1 more token then you can win per spin

Answer 2

Option D- The expected value is -0.5, and the game is not fair. So the player will lose about 0.5 tokens for a single spin over time.

Explanation:

Given : At a County fair there is a spinner game with 12 sectors: 2 red sectors, 2 green sectors, 2 blue sectors, and 6 yellow sectors.

If the spinner lands on :

A red sector- the player wins 2 tokens.

A green sector- the player wins 2 tokens.

A blue sector- the player wins 2 tokens.

A yellow sector- the player loses 3 tokens.

To find : Is this game fair for the player and how much will the player win or lose on an average over time?

Solution :

First we find the probability of each sector,

`\text{Probability}=\frac{\text{Favorable outcome}}{\text{Total number of outcome}}`

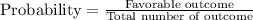
Total outcome = 12

1)
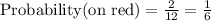
`\text{Probability(on red)}=(2)/(12)=(1)/(6)`

2)
`\text{Probability(on green)}=(2)/(12)=(1)/(6)`

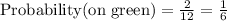
3)
`\text{Probability(on blue)}=(2)/(12)=(1)/(6)`

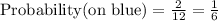
4)
`\text{Probability(on yellow)}=(6)/(12)=(1)/(2)`

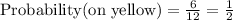
Now, For a win the profit is w=2 tokens.

For a loss, the profit is l= -3 tokens.

Now, The expected value is the product of probability and its profit/loss.

`E(x)=P(R)* w+P(G)* w+P(B)* w+P(Y)* l`

`E(x)=(1)/(6)* 2+(1)/(6)* 2+(1)/(6)* 2+(1)/(2)* (-3)`

`E(x)=(1)/(3)+(1)/(3)+(1)/(3)-(3)/(2)`

`E(x)=1-(3)/(2)`

`E(x)=-(1)/(2)`

`E(x)=-0.5`

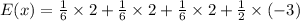
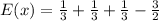
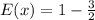
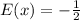
Therefore, The game is not fair. So the player will lose about 0.5 tokens for a single spin over time.

Hence, Option D is correct.