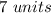Question

What is the x-coordinate of the point that divides the directed line segment from K to J into a ratio of 1:3?

–1
3
7
11

Answer 1

Since we need a point that divides K-->J into two segments in a 1:3 ratio, let's flip it to a 3:1 ratio in the J-->K direction. That means that this point is 3/(3+1) = 3/4 of the way up line JK.
Let's take 3/4 of the x of K (plus the 1 for the x of J):
3/4×(9 - 1) + 1 (because the beginning ofvthe line, at J, has an x of 1)...
3/4×(8) + 1 = 6 + 1 = 7
Therefore the answer is C) 7

Answer 2

Step 1

Find the distance KJ in the x-coordinate

we know that

the distance between two points with only one coordinate is equal to

`d=\left|x_2-x_1\right|`

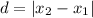
substitute the values

`d=\left|9-1\right|=8\ units`

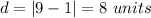
Step 2

Find the x-coordinate of the point that divides the directed line segment from K to J into a ratio of
`1:3`

we know that

the ratio is
`1:3`

so

`1+3=4`

Divided the distance KJ in the x-coordinate by
`4`

`8/4=2\ units`

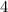
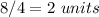
Adds the x-coordinate of J to
`3` times
`2\ units`

`1+3*(2)=7\ units`

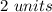
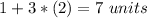
therefore

the answer is the option

`7\ units`