Question

State the degree and leading coefficient of each polynomial in one variable. If it is not a polynomial in one variable, explain why.

Answer 1

Given:

`(2x-1)(4x^2+3)`

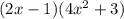
The degree of the polynomial is the highest exponent in a polynomial.

To find the degree of the polynomial, let's simplify the given expression.

We have:

`(2x-1)(4x^2+3)`

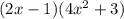
Apply distributive property:

`\begin{gathered} 2x(4x^2)+2x(3)-1(4x^2)-1(3) \\ \\ 8x^3+6x-4x^2-3 \\ \\ 8x^3-4x^2+6x-3 \end{gathered}`

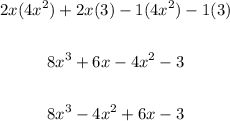
The highest exponent of the polynomial is 3.

Therefore, the polynomial is a third degree polynomial.

The leading coefficient is the coefficient of the highest exponent which is also the first term.

Therefore, the leading coefficient is 8

ANSWER:

Degree of the polynomial = 3

Leading coefficient = 8