Question

The weight of a medium-sized orange selected at random from a large bin of oranges at a local supermarket is a normally distributed random variable with mean μ = 12 ounces and standard deviation σ = 1.2 ounces. suppose we independently select two oranges at random from the bin. what is the probability that the difference in the weights of the two oranges exceeds 3 ounces?

Answer 1

0.0392

Explanation:

The weight is normally distributed with :

Mean (\mu)= 12 ounces

Standard deviation (\sigma ) = 1.2 ounces

Let X_1 be the weight of first orange and X_2 be the weight of second orange.

Let X be the difference of the weight of two oranges (X_1-X_2)

X_1(12,1.2^{2}) and X_2(12,1.2^{2})

X(12-12,√1.2^{2}+1.2^{2}) = X(0,1.6971)

We need to calculate P(X>3) = 1-P(X≤3)

For calculating P(X≤3) in normal distribution, we use

Z =
`(X-\mu)/(\sigma )`

=
`(3-0)/(1.6971)`

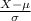
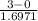
= 1.7677

P(Z≤ 1.7677) = 0.9608 (From normal distribution table)

P(X > 3) = 1-0.9608

= 0.0392

Answer 2

Let
`X_1` and
`X_2` represent the weights of the two oranges.
Let
`d=X_1-X_2` represent the difference in weight.
We're given that

`X_1` ~ N(12, 1.2^2)

`X_2` ~ N(12, 1.2^2)

Then,


Let's find

`P(d\ \textgreater \ 3) = 1 - \phi ( (3-0)/(1.6971)) = 1- 0.9615 = 0.0385`

So the answer is 0.0385