Question

Vector V is 448 m long in a224° direction. Vector Wis336 m long in a 75.9°direction.Find the direction of theirvector sum.

Answer 1

In order to find the direction of the vector sum, first let's calculate the horizontal and vertical components of each vector:

`\begin{gathered} V_x=V\cos\theta\\ \\ V_x=448\cos224°\\ \\ V_x=-322.26 \end{gathered}`
`\begin{gathered} V_y=V\sin\theta\\ \\ V_y=448\sin224°\\ \\ V_y=-311.21 \end{gathered}`
`\begin{gathered} W_x=W\cos\theta\\ \\ W_x=336\cos75.9°\\ \\ W_x=81.85 \end{gathered}`
`\begin{gathered} W_y=W\sin\theta\\ \\ W_y=336\sin75.9°\\ \\ W_y=325.88 \end{gathered}`

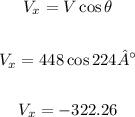
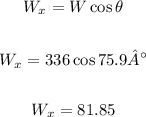
Now, let's add the horizontal components together and the vertical components together:

`\begin{gathered} S_x=V_x+W_x=-322.26+81.85=-240.41\\ \\ S_y=V_y+W_y=-311.21+325.88=14.67 \end{gathered}`

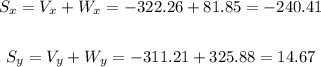
To calculate the direction of the vector sum S, we can use the formula below:

(Since Sx is negative and Sy is positive, the direction is in quadrant II)

`\begin{gathered} \theta_S=\tan^(-1)((S_y)/(S_x))\\ \\ \theta_S=\tan^(-1)((14.67)/(-240.41))\\ \\ \theta_S=\tan^(-1)(-0.0610207)\\ \\ \theta_S=176.51° \end{gathered}`