Question

State the image of the point (-2, -1) after a reflection across the line y = 1.Blank 1:Blank 2:

Answer 1

You have to reflect point (-2,-1) across the line y=1

A reflection over any line parallel to the x-axis implicates that you have to change the y-coordinate on the preimage, leaving the x-coordinate the same.

The first step is to determine the vertical distance between the line y=1 and the point (-2,-1), to do so you have to calculate the difference between y=1 and the y-coordinate y=-1:

`\begin{gathered} d=1-(-1) \\ d=1+1 \\ d=2 \end{gathered}`

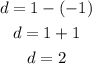
The vertical distance between the preimage and the line of reflection is two units.

The next step is to move the point the same vertical distance above the line of reflection:

The coordinates of the point (-2,-1) after a reflection over the line y=1 are (-2,3)