Question

Let $f(x) = x^{10}+5x^9-8x^8+7x^7-x^6-12x^5+4x^4-8x^3+12x^2-5x-5$.

Answer 1

The remainder when
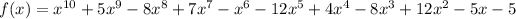`\(f(x) = x^(10) + 5x^9 - 8x^8 + 7x^7 - x^6 - 12x^5 + 4x^4 - 8x^3 + 12x^2 - 5x - 5\)` is divided by
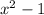`\(x^2 - 1\)` is 0.

Given the polynomial
`\(f(x) = x^(10) + 5x^9 - 8x^8 + 7x^7 - x^6 - 12x^5 + 4x^4 - 8x^3 + 12x^2 - 5x - 5\)`.

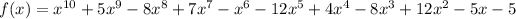1. Remainder when divided by x - 1:

Substitute x = 1 into f(x):

`\[ f(1) = 1^(10) + 5(1)^9 - 8(1)^8 + 7(1)^7 - (1)^6 - 12(1)^5 + 4(1)^4 - 8(1)^3 + 12(1)^2 - 5(1) - 5 \]`

f(1) = 0

2. Remainder when divided by x + 1:

Substitute x = -1 into f(x):

`\[ f(-1) = (-1)^(10) + 5(-1)^9 - 8(-1)^8 + 7(-1)^7 - (-1)^6 - 12(-1)^5 + 4(-1)^4 - 8(-1)^3 + 12(-1)^2 - 5(-1) - 5 \] \[ f(-1) = 14 \]`

3. Remainder when divided by
`\(x^2 - 1\)`:

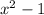The remainder is the product of the remainders from steps 1 and 2:

`\[ \text{Remainder} = R_1 * R_2 = 0 * 14 = 0 \]`

Therefore, the remainder when
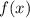`\(f(x)\)` is divided by
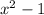`\(x^2 - 1\)` is 0.

The complete question is:
Let f(x) =
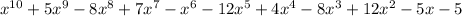`x^(10)+5x^9-8x^8+7x^7-x^6-12x^5+4x^4-8x^3+12x^2-5x-5` find the remainder when is divided by
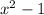`x^2 -1`.