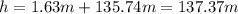ANSWER
137.37 m
Step-by-step explanation
Let's draw a diagram of this situation first,
As we can see, there is a right triangle formed by the tower and your eye level. We know that the distance between the ground and your eye is 1.63m, so the height of the tower is,
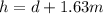
Using trigonometric ratios we can find the vertical distance from your eye to the top of the tower, d. We know the angle from your eye to the top of the tower, the distance between you and the base of the tower (which is the adjacent side of the angle) and we want to find the opposite side to the given angle. We use the tangent of the angle,
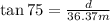
Solving for d,
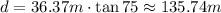
Hence, the height of the tower is,