Answer:
a) the line of symmetry for f(x) and g(x) is the same (x = -3)
b) The y-intercept of f is greater than the y-intercept of g
c) the average rate of change for f is less than the rate of change of g
Step-by-step explanation:
Given:
A table describing functon f(x) and a parabola describing function g(x)
To find:
we need to complete the statements by filling in the blanks
a) The first is to determine the line of symmetry of f and g
The line of symmetry is the value of x which divides the parabola into equal halves (mirror images)
It is also the x coordinate of the vertex of the parabola. Since we are comparing f and g, it means plotting the points on the table will give a parabola.
Graph of f(x) showing the line of symmetry:
Graph of function g(x):
From the digrams above, the line of symmetry for f(x) and g(x) is the same (x = -3)
b) the y-intercept is the value of y when x = 0
On a graph, it is the value of y when the line crosses the y axis
On the graph of f(x), the line crosses the y axis at y = -2
Hence, the y-intercept is -2
On the table for f(x), x = 0 when f(x) = 8
On graph of f(x), the line crosses the y axis at y = 8
Hence, the y-intercept is 8
8 > -2
The y-intercept of f is greater than the y-intercept of g
c) The rate of change of a function is given as:
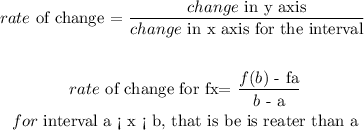
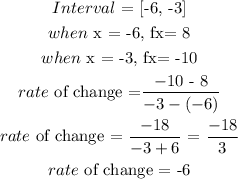
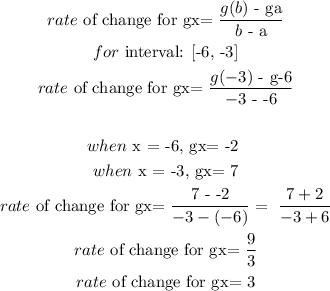
rate of change for f against g: -6 < 3
Over the interval [-6, -3], the average rate of change for f is less than the rate of change of g