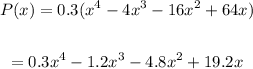Question

The question is the image The polynomial of degree 4, P(x) P(x), has a root of multiplicity 2 at x=4 x=4 and roots of multiplicity 1 at x=0 x=0 and x=-4 . It goes through the point (5,13.5) .Find a formula for P(x) .

Answer 1

Answer:
`P(x)=0.3x^4-1.2x^3-4.8x^2+19.2x`

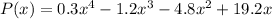
Step-by-step explanation:

Given that the polynomial is of degree 4

Since it has a root of multiplicity 2 at x = 4

`(x-4)^2\text{ is a factor}`

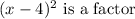
Roots of multiplicity 1 at x = 0

`\begin{gathered} x\text{ is a factor} \\ (x+4)\text{ is another factor} \end{gathered}`

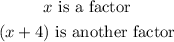
Combining these, we have:

`\begin{gathered} P(x)=A(x)(x+4)(x-4)^2 \\ \\ =A(x^4-4x^3-16x^2+64x) \end{gathered}`

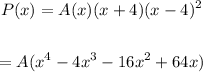
To find the value of A, we use the given point (5, 13.5)

x = 5, P(x) = 13.5

`\begin{gathered} 13.5=A(5^4-4*5^3-16*5^2+64*5) \\ \\ 13.5=45A \\ \\ A=(13.5)/(45)=0.3 \end{gathered}`

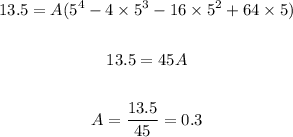
Now, we have:

`\begin{gathered} P(x)=0.3(x^4-4x^3-16x^2+64x) \\ \\ =0.3x^4-1.2x^3-4.8x^2+19.2x \end{gathered}`