Question

How many times does the graph of the function below intersect or touch the x-axis? y= -x^2+x+6

Answer 1

2 times, once at 3 and once at -2

Answer 2

Graph of the function touches x-axis twice at 3 and -2.

Explanation:

Given : Quadratic function
`y= -x^2+x+6`

To find : How many times does the graph of the function given intersect or touch the x-axis?

Solution :

To find the points graph touch the x-axis i.e, the functions real roots.

Using quadratic formula,

General form -
`ax^2+bx+c=0`

`D=b^2-4ac`

Solution is
`x=(-b\pm√(D))/(2a)`

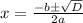
Equation is
`y= -x^2+x+6`

where, a=-1 , b=1, c=6

`D=b^2-4ac`

`D=(1)^2-4(-1)(6)`

`D=1+24`

`D=25`

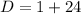
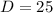
D>0 i.e, 2 real roots exist.

Solution is
`x=(-b\pm√(D))/(2a)`

`x=(-(1)\pm√(25))/(2(1))`

`x=(1\pm 5)/(2)`

`x=3,-2`

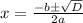
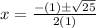
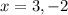
Therefore, graph of the function touches x-axis twice at 3 and -2.

Refer the attached figure below.