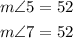Question

Two parallel lines are cut by a transversal as shown below. Suppose m<2= 128 degrees. Find m<5 and m<7

Answer 1

From the diagram given we notice that angle 2 and angle 4 are vertical opposite angles, which means that the are equal, that is:

`m\angle2=m\angle4`

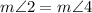
and hence we have that:

`m\angle4=128`

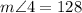
We also notice that angles 4 and 5 are consecutive interior angles, and since the lines are parallel this means that they have to add to 180°:

`m\angle4+m\angle5=180`

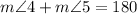
Plugging the value of angle 4 and solving for angle 5 we have:

`\begin{gathered} 128+m\angle5=180 \\ m\angle5=180-128 \\ m\angle5=52 \end{gathered}`

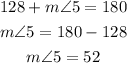
Finally, we notice that angles 5 and 7 are vertically opposite which means they are equal, hence:

`m\angle7=52`

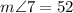
Therefore, we conclude that:

`\begin{gathered} m\angle5=52 \\ m\angle7=52 \end{gathered}`