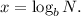Answer: The required logarithmic form of the given equation is
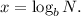
Step-by-step explanation: We are given to express the following equation in logarithmic form :

We know that
The logarithmic form of an exponential equation
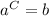 is given by
is given by
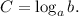
So, from equation (i), we get
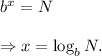
Thus, the required logarithmic form of the given equation is