Question

A 10.7 m solution of NaOH has a density of 1.33 g/cm3 at 20 °C. Calculate thefollowing:(a) the mole fraction of NaOH(b) the weight percent of NaOH(c) the molarity of the solution

Answer 1

a) 0.162.

b) 0.230.

c) 10 M.

Step-by-step explanation:

a) 10.7 m indicates that e have 10.7 mol/kg of NaOH. ÑSo let's find the number of moles of water based on 1 kg of water (1000 g) of watr. The molar mass of watrr ois 18 g/mol:

`1000\text{ g H}_2O\cdot\frac{1\text{ mol H}_2O}{18\text{ g H}_2O}=55.5\text{ moles H}_2O.`

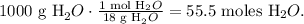
The total number of moles, in this case, would be the sum of moles of NaOH and the sum of moles of water: 55.5 moles + 10.7 moles = 66.2 moles. The mole fraction of NaOH is:

`mole\text{ fraction of NaOH=}\frac{nimbe\text{r of moles of NaOH}}{total\text{ number of moles}}=\frac{10.7\text{ moles}}{66.2\text{ moles}}=0.162.`

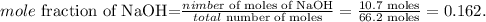
The mole fraction of NaOH is 0.162.

b) To find the weight percent of NaOH, we have to find the mass of NaOH and the mass of water. The mass of NaOH can be found using its molar mass which is 40 g/mol, like this:

`10.7\text{ moles NaOH}\cdot\frac{40\text{ g NaOH}}{1\text{ mol NaOH}}=428\text{ g NaOH.}`

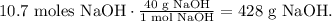
And as we saw before, the mass of water would be 1 kg (1000 g). So the total mass would b the mass of NaOH and the mass of H2O : 1000 g + 428 g = 1428 g. The weight percent of NaOH is:

`weight\text{ }\%\text{ of NaOH=}\frac{mas\text{s of NaOH}}{total\text{ mass}}=\frac{428\text{ g}}{1428}=0.230.`

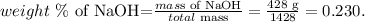
The weight percent of NaOH is 0.230.

c) Finally, to calculate the molarity of the solution, we have to find the moles of solute and liters of solution, because the formula of molarity is:

`Molarity\text{ \lparen M\rparen=}\frac{mole\text{s of solute}}{liter\text{s of solution}}=(mol)/(L).`

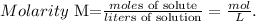
We already know the moles of solute, ie the moles of NaOH, which is 10.7 moles. But, we have to find the volume in liters of solution. In this case, we have to use the given density. The mass of the solution as we saw before, is 1428 g. The calculaton is:

`volume=(mass)/(density)=\frac{1428\text{ g}}{1.33(g)/(cm^3)}=1074\text{ cm}^3.`

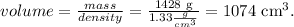
But we have to convert cm^ to liters. Remember that 1 liter equals 1000 cm^3:

`1074\text{ cm}^3\cdot\frac{1\text{ L}}{1000\text{ cm}^3}=1.07\text{ L.}`

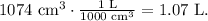
And the final step is to replace the obtained values in the molarity formula, like this:

`Molarity=\frac{mole\text{s of NaOH}}{liter\text{s of solution}}=\frac{10.7\text{ moles}}{1.07\text{ L}}=10\text{ M \lparen}(mol)/(L)).`

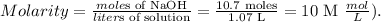
The molarity of the solution would be 10 M.