Question

Use the principle of inclusion and exclusion to find the number of positive integers less than 1,000,000 that are not divisable by 6 or 4

Answer 1

This is a simple problem based on combinatorics which can be easily tackled by using inclusion-exclusion principle.
We are asked to find number of positive integers less than 1,000,000 that are not divisible by 6 or 4.
let n be the number of positive integers.
∴ 1≤n≤999,999
Let c₁ be the set of numbers divisible by 6 and c₂ be the set of numbers divisible by 4.
Let N(c₁) be the number of elements in set c₁ and N(c₂) be the number of elements in set c₂.

∴N(c₁) =
`(999,999)/(6) = 166666`
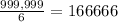
N(c₂) =
`(999,999)/(4) = 250000`
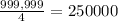
∴N(c₁c₂) =
`(999,999)/(24) = 41667`
∴ Number of positive integers that are not divisible by 4 or 6,

N(c₁`c₂`) = 999,999 - (166666+250000) + 41667 = 625000
Therefore, 625000 integers are not divisible by 6 or 4