Question

find the coordinates of point P along the directed line segment AB so that AP to PB is the given radio.

Answer 1

The given points are:

A = (8, 0)

B = (3, 22)

We need to find the point P that divides the segment AB so that AP to PB is 1:4

Let's say

(x1, y1) = (8, 0)

(x2, y2) = (3, 22)

First ratio = m1 = 1

Second ratio = m2 = 4

To find the missing coordinates of P (x,y), we will use the section formula, that is:

`(x,y)\text{ = (}\frac{m1x2+\text{ m2x1}}{m2+m1},\frac{m1y2\text{ + m2y1}}{m2+m1}\text{)}`

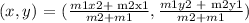
Now, by solving it

`(x,y)\text{ = (}\frac{1\cdot3+\text{ 4}\cdot8}{4+1},\frac{1\cdot22\text{ + 4}\cdot0}{4+1}\text{)}`
`(x,y)\text{ = (}(3+32)/(5),\frac{22\text{ + }0}{5}\text{)}`
`(x,y)\text{ = (}(35)/(5),\frac{22\text{ }}{5}\text{)}`
`(x,y)\text{ = (7},4.4\text{)}`

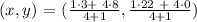
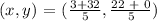
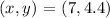
Hence, the coordinates of point P are (7, 4.4).