Question

HELP ASAP 29 POINTS A function, f, passes through the points (1,1), (2,7) and (3,25). A function, g, passes through the points (1,36), (2,43) and (3,50).

As the value of x increases, the values of f(x) and g(x) remain constant.



As the value of x increases, the value of f(x) will never exceed the value of g(x).



As the value of x increases, the value of f(x) will eventually exceed the value of g(x).



As the value of x increases, the value of f(x) and the value of g(x) both approach 100

Answer 1

As the value of x increases, the value of f(x) will never exceed the value of g(x).

Answer 2

Answer with explanation:

≡≡It is given that , function, f, passes through the points (1,1), (2,7) and (3,25).

Slope between two points is given by the formula

`=(y_(2)-y_(1))/(x_(2)-x_(1)) \text{Having coordinates} ,(x_(1),y_(1)),(x_(2),y_(2))`

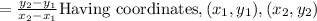
→→You will find that,

`(7-1)/(2-1)=6, \text{and} (25-7)/(3-2)=18 \text{and} (25-1)/(3-1)=12`

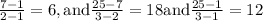
The slopes are not same.So, the given function is not linear.

Also, f(1)=1, f(2)=7,f(3)=25

1+6=7+18=25,f(x) increases each time differently ,first by a number of ,6 ,then by 18,may be then by 54,....with increase in value of x , by 1 unit.

≡≡The function, g, passes through the points (1,36), (2,43) and (3,50).

Slope between two points is

`(43-36)/(2-1)=(50-43)/(3-2)=(50-36)/(3-1)=7`

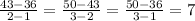
36 +7=43+7=50+7=57

So,the function is linear.

f(x) increases each time with same digit,that is by value of 7, with increase in value of x , by 1 unit.

Option C:⇒As the value of x increases, the value of f(x) will eventually exceed the value of g(x).