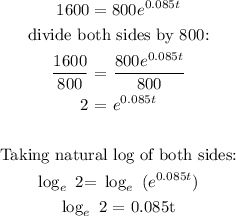Question

Attached is my question. To the nearest tenth of a year

Answer 1

8.2 years

Step-by-step explanation:

Initial amount = $800

Doubling the amount = 2(800) = $1600

Future amount = double the amount = $1600

rate = 8.5% = 0.05

time = t = ?

n = compounded continously

The function is given as:

`A=800e^(0.085t)`

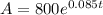
We need to find the time given the amount is $1600:

`\begin{gathered} 1600=800e^(0.085t) \\ \text{divide both sides by 800:} \\ (1600)/(800)\text{ = }(800e^(0.085t))/(800) \\ 2\text{ = }e^(0.085t) \\ \\ \text{Taking natural log of both sides:} \\ \log _e\text{ 2= }\log _e\text{ }(e^(0.085t)) \\ \log _e\text{ 2 = 0.085t} \end{gathered}`
`\begin{gathered} \log _e\text{ = ln} \\ \log _e\text{ 2 = ln 2} \\ \ln 2\text{ = 0.085t} \\ divide\text{ both sides by 0.085:} \\ \frac{\ln \text{ 2}}{0.085\text{ }}\text{ = }\frac{\text{0.085t}}{0.085} \\ 8.1547\text{ = t} \\ \\ To\text{ the nearest tenth of a year, t = 8.2 years} \end{gathered}`