Question

The equation of a circle is x2 + y2 + 6x + 4y + 10 = 1. What is this equation written in its standard form?

Answer 1

You need to complete the square in x and in y,


`x^(2) + y^(2) + 6x + 4y + 10 = 1`

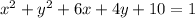
First, group the x-terms and the y-terms separately.


`x^(2) + 6x + y^(2) + 4y + 10 = 1`

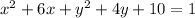
Move the 10 to the right side by subtracting 10 from both sides.


`x^(2) + 6x + y^(2) + 4y = -9`

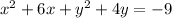
Now complete the square in x and in y.
The constant you need to add to complete each square is the square of half of the coefficient of the x or y term. Make sure to add the constants to both sides of the equation.


`x^(2) + 6x + 9 + y^(2) + 4y + 4= -9 + 9 + 4`


`(x + 3)^(2) + (y + 2)^(2) = 4`