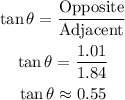Question

Consider the right triangle shown below that has an interior angle measure of θ radians.(a)The vertical leg of the triangle is how many times as long as the hypotenuse of the triangle?_____ times as long   (b)What is the value of sin(θ)? sin(θ)=   (c)The horizontal leg of the triangle is how many times as long as the hypotenuse of the triangle? _____times as long   (d)What is the value of cos(θ)? cos(θ)= (e)The vertical leg of the triangle is how many times as long as the horizontal leg of the triangle? ______times as long   (f)What is the value of tan(θ)? tan(θ)=

Answer 1

Part A

The vertical leg of the triangle = 1.01 cm

The hypotenuse = 2.1 cm

`(1.01)/(2.1)=0.48`

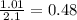
• 0.48 times as long

Part B

`\begin{gathered} \sin \theta=\frac{\text{Opposite}}{\text{Hypotenuse}} \\ \sin \theta=(1.01)/(2.1) \\ \sin \theta\approx0.48 \end{gathered}`

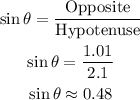
Part C

The horizontal leg of the triangle = 1.84 cm

The hypotenuse = 2.1 cm

`(1.84)/(2.1)\approx0.88`

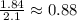
• 0.88 times as long

Part D

`\begin{gathered} \cos \theta=\frac{\text{Adjacent}}{\text{Hypotenuse}} \\ \cos \theta=(1.84)/(2.1) \\ \cos \theta\approx0.88 \end{gathered}`

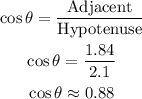
Part E

The vertical leg of the triangle = 1.01 cm

The horizontal leg of the triangle = 1.84 cm

`(1.01)/(1.84)\approx0.55`

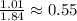
• 0.55 times as long

Part F

`\begin{gathered} \tan \theta=\frac{\text{Opposite}}{\text{Adjacent}} \\ \tan \theta=(1.01)/(1.84) \\ \tan \theta\approx0.55 \end{gathered}`