Answer:
Option 2nd is correct
Explanation:
To graph the given inequality, graph the boundary of these equations.
Use dashed line if < or > used to indicate that the boundary is not the part of the solution.
Use solid line if ≤ or ≥ used to indicate that the boundary is included in the solution.
Given the system of inequalities:
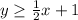

First graph the inequality
 .
.
The related equation is
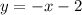 .
.
Since this is strict inequality '>', so the border is dotted.
x-intercept:
Substitute value y=0 in
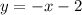 to solve for x
to solve for x
0 = -x-2
x = -2
x-intercept = (-2, 0)
y-intercept
Substitute value x=0 in
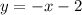 to solve for y
to solve for y
y= 0-2
y = -2
y-intercept = (0, -2)
Since the sign of inequality is >, therefore the point on the line does not contains the solution set and shade the upper half of the line.
Now, graph the inequality
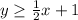 .
.
The related equation is
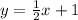
Since, this inequality is '≥' not the strict one, the border line is solid.
x-intercept:
Substitute value y=0 in
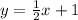 to solve for x
to solve for x
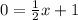
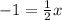
⇒x = -2
x-intercept = (-2, 0)
y-intercept
Substitute value x=0 in
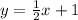 to solve for y
to solve for y
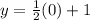
y =1
y-intercept = (0, 1)
Since the sign of inequality is ≥ , therefore the point on this line contain in the solution set and shade the upper half of the line.
You can see the graph of these system of inequalities.