Question

Use lagrange multipliers to find the point on the plane x − 2y + 3z = 6 that is closest to the point (0, 2, 5).

Answer 1

Lagrangian:


`L(x,y,z,\lambda)=x^2+(y-2)^2+(z-5)^2+\lambda(x-2y+3z-6)`

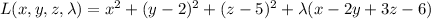
where the function we want to minimize is actually
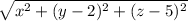
`√(x^2+(y-2)^2+(z-5)^2)`, but it's easy to see that
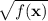
`√(f(\mathbf x))` and
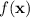
`f(\mathbf x)` have critical points at the same vector
`\mathbf x`.

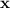
Derivatives of the Lagrangian set equal to zero:


`L_x=2x+\lambda=0\implies x=-\frac\lambda2`

`L_y=2(y-2)-2\lambda=0\implies y=2+\lambda`

`L_z=2(z-5)+3\lambda=0\implies z=5-\frac{3\lambda}2`

`L_\lambda=x-2y+3z-6=0`

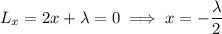
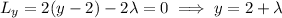
Substituting the first three equations into the fourth gives


`-\frac\lambda2-2(2+\lambda)+3\left(5-\frac{3\lambda}2\right)=6`

`11-7\lambda=6\implies \lambda=\frac57`

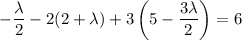
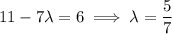
Solving for
`x,y,z`, we get a single critical point at
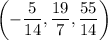
`\left(-\frac5{14},\frac{19}7,(55)/(14)\right)`, which in turn gives the least distance between the plane and (0, 2, 5) of
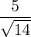
`\frac5{√(14)}`.