Question

A group of 13 people is randomly selected to discuss products of the Yummy Company. It is determined that the mean number (per group) who recognize the Yummy brand name is 10.2 and the standard deviation is 0.84. Would it be unusual to randomly select 13 people and find that fewer than 7 recognize the Yummy brand?

Answer 1

GIVEN;

We are told that a group of 13 people is selected and it is determined that the mean number who recognize the Yummy brand name is 10.2, and the standard deviation is 0.84.

Required;

To determine if it would be unusual to randomly select 13 people and find that "fewer than 7" recognize the Yummy brand.

Step-by-step solution;

First of all, take note of the information provided;

`\begin{gathered} \mu(mean)=10.2 \\ \\ \sigma(standard\text{ }deviation)=0.84 \\ \\ n(sample\text{ }size)=13 \end{gathered}`

We shall determine this as shown below;

`\mu\pm2\sigma`

Note that by "UNUSUAL" as indicated in the question, we need to know a data value that is more than 2 standard deviations away from the mean in either the positive direction or the negative direction (that is, plus or minus).

Therefore the range of what is considered usual will be within the expression set up above.

We now have;

`\begin{gathered} \mu\pm2\sigma \\ Therefore: \\ \\ 10.2\pm2(0.84)=10.2\pm1.68 \end{gathered}`

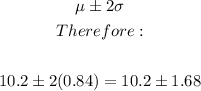
We now have two values which are;

`\begin{gathered} Highest\text{ }value=10.2+1.68=11.88 \\ \\ Lowest\text{ }value=10.2-1.68=8.52 \\ \\ Therefore: \\ \\ Usual\text{ }range:8.52\leq x\leq11.88 \end{gathered}`

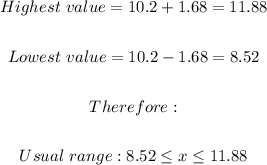
To find that fewer than 7 recognize the Yummy brand would be unusual because the result here shows that you expect to find at least 8.52. The value 7 is already short of this value and therefore, it would be unusual to find that number in your research results.

ANSWER:

Yes, it would be unusual.