Question

Which expressions are equivalent to the one below? Check all that apply. 21^x/3^x

A.(21/3)^x
B.7
C.7^x
D.(21 - 3)^x
E.7^x*3^x/3^x
F.3^x

Answer 1

(A), (C) and (E)

Explanation:

The given expression is:

`(21^x)/(3^x)`

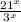
(A) The expression is:

`((21)/(3))^x`

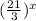
Now, this expression can be written as:

`(21^x)/(3^x)`

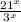
which is equivalent to the given expression, thus this option is correct.

(B) The expression is:

`7`

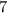
The above given expression that is
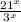`(21^x)/(3^x)` can be written as:

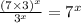`((7*3)^x)/(3^x)=7^x` which is not equivalent, thus this option is incorrect.

(C) The given expression is:

`7^x`

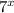
The above given expression that is
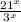`(21^x)/(3^x)` can be written as:

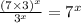`((7*3)^x)/(3^x)=7^x` which is equivalent, thus this option is correct.

(D) The given expression is:

`(21-3)^x`

which can be solved as
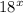`18^x` which is not equivalent to the given expression, therefore this option is incorrect.

(E) The given expression is:

`(7^x*3^x)/(3^x)`

which can be written as:

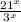`(21^x)/(3^x)` which is equivalent to the given expression, thus this option is correct.

(F) The given expression is:

`3^x`

which is not equivalent to the given expression, thus this option is incorrect.

Answer 2

options: A,C,E are correct.

Explanation:

We have to find the expression equivalent to the expression:

`(21^x)/(3^x)`

we know that:
`21^x=(3*7)^x\\\\21^x=3^x*7^x`

Hence,

`(21^x)/(3^x)=(3^x*7^x)/(3^x)=7^x`-----(1)

A)
`((21)/(3))^x= 7^x` (same as(1))

Hence, option A is correct.

B) 7 ; which is a different expression from (1)

Option B is incorrect.

C)
`7^x` (Same as (1))

Option C is correct.

D)
`(21-3)^x=18^x` which is a different expression from (1)

Hence, option D is incorrect.

E)
`(7^x*3^x)/(3^x)=7^x` ; which is same as (1)

Hence, Option E is correct.

F)
`3^x` ; which is not same as expression (1)

Hence, option F is incorrect.