Question

find the midpoint of PQ with endpoints P(0,2) and Q(6,2). Then write an equation of the line that passes through the midpoint and is perpendicular to PQ.

Answer 1

Given the end points of the line PQ, consider the figure given below,

Using the mid point formula, the coordinates of the mid point is calculated as,

`x=(0+6)/(2)=(6)/(2)=3`
`y=(2+(-2))/(2)=0`

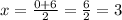
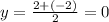
Thus, the coordinates of the mid point is (3,0). Let this point be named R.

Now, we need to find the equation of the line perpendicular to PQ and passing through R. Since perpendicularity is concerned, we will the concept of slopes.

First we have to find the slope of line PQ,

`\text{Slope of PQ=}(-2-2)/(6-0)=(-4)/(6)=(-2)/(3)`

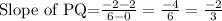
We know that the product of slopes of two perpendicular lines is -1, so the slope of the perpendicular line becomes,

`m=(-1)/(((-2)/(3)))=(3)/(2)`

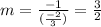
So we know that the perpendicular line has a slope 'm' and passes through R (3,0).

Therefore, we can use the point slope form of the straight line equation,

`y-0=(3)/(2)(x-3)\Rightarrow2y=3x-9\Rightarrow3x-2y-9=0`

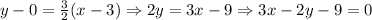
Thus, the equation of the required line is 3x - 2y - 9 = 0.