Question

A diver 20 feet below the surface of the water starts to ascend at 1/2 foot per second. A turtle that started 11 feet below the surface descends at a rate of 1/4 foot per second. Write an equation to model the position of 1/4 each. Write an equation to model the position of each. When are they at the same position? What is that position?

Answer 1

To solve this, we need to create a system of equations to model the position of the diver and the turtle.

Let's say that 0 ft is the surface of the water. Then the diver is at -20ft. Also, it's position rises 1/2 ft per second. This in an equation would be:

`D(t)=(1)/(2)t-20`

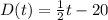
For each second, the altitude rises by 1/2 ft, starting from -20ft.

Now for the turtle is similar, but the turtle descends instead of rising which means the sign is negative, and the starting position is at -11ft:

`T(t)=-(1)/(4)t-11`

They will be on the same position when the two positions are equal, thus:

`D(t)=T(t)\Rightarrow(1)/(2)t-20=-(1)/(4)t-11`

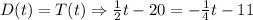
And solve for t:

`\begin{gathered} (1)/(2)t-20=-(1)/(4)t-11 \\ (1)/(2)t+(1)/(4)t=20-11 \\ (3)/(4)t=9 \\ t=9\cdot(4)/(3) \\ t=12 \end{gathered}`

They will meet at 12 seconds.

To find the position where they'll meet we just evaluate either of the equations in t = 12s:

`\begin{gathered} D(12)=(1)/(2)\cdot12-20=-14 \\ T(12)=-(1)/(4)\cdot12-11=-14 \end{gathered}`

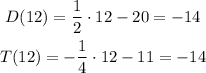
They meet at -14ft or 14 ft below the surface,