Question

Identify the zeros and state their multiplicities describe the effect on the graph #7

Answer 1

Step-by-step explanation:

Here, we want to get the zeros, multiplicity, and effect of the zeros of the polynomial

To get this, we can set the function to zero and factorize it

Mathematically, we have that as:

`x^2(x^2-2x-8)\text{ = 0}`

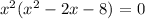
We can further have the equation broken down as follows:

`\begin{gathered} x^2((x+2)(x-4))=\text{ 0} \\ x^2=0 \\ x+2\text{ = 0} \\ x-4=0 \\ x\text{ = 0 twice, -2 , 4} \end{gathered}`

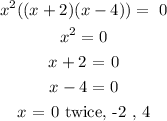
Now, let us get the effect of these zeros on the graph

As we can see, only x = 0 has an even multiplicity (2), x = -2, and 4 have an odd multiplicity

When there is an even multiplicity, the zero will touch the the graph, but when there is an odd multiplicity, the graph will cut through the x-axis at that point

Thus, we can conclude that:

At x = 0, the curve or graph will touch the x-axis and bounce off

At x = -2, the graph will cut through the point x = -2

At x = 4 , the graph will cut through the point x = 4