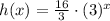We want the answer in exponential form:
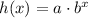
where a and b are the constants to be determined. We can find a and b by substituting the given points and construct a system of equatons, that is, by replacing point (1,16) we have

and by substituting point (5,1296), we get
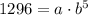
Then, we have 2 equations in 2 unknonws:
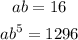
By isolating a from the first equation and substituting this result into the second one, we get
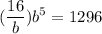
which gives
![\begin{gathered} 16b^4=1296 \\ b^4=(1296)/(16) \\ b^4=81 \\ b=\sqrt[4]{81} \\ b=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/qjztntybf1hahgovcb8y.png)
Then, by substituting this result into the first equation of our system, we obtain

Therefore, the answer is