Question

A 70 kg diver is standing on a 26m high cliff. What is his potential energy at the top of the cliff? When he is half way to the water, how much potential energy does he have? When he is halfway how much kinetic energy does he have? Just before the diver hits the water, how much kinetic energy does he have?

Answer 1

Given data:

* The mass of the diver is m = 70 kg.

* The height of the cliff is h = 26 m.

Solution:

(a). The potential energy of the diver at the top of the cliff is,

`U=\text{mgh}`

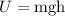
where g is the acceleration due to gravity,

Substituting the known values,

`\begin{gathered} U=70*9.8*26 \\ U=17836\text{ J} \end{gathered}`

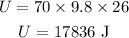
Thus, the potential energy at the top of the cliff is 17836 J.

(b). The potential energy at halfway to the water is,

`U_1=\text{mg}*(h)/(2)`

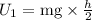
By simplifying,

`\begin{gathered} U_1=(mgh)/(2) \\ U_1=(U)/(2) \\ U_1=(17836)/(2) \\ U_1=8918\text{ J} \end{gathered}`

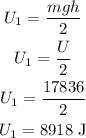
Thus, the potential energy of the diver in the halfway is 8918 J.

(c). The diver is at rest at the top of the hill, thus, the kinetic energy of the diver at the top of the hill is,

`K=0\text{ J}`

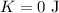
Thus, the net energy at the top of the cliff is,

`\begin{gathered} E=U+K \\ E=17836+0_{} \\ E=\text{17836 J} \end{gathered}`

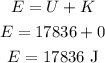
According to the law of conservation of energy, the net energy of the system remains the same at halfway as at the top of the cliff.

Thus, the kinetic energy at halfway is,

`\begin{gathered} E=U_1+K_1 \\ K^{}_1=E-U_1 \\ K_1=17836-8918 \\ K_1=8918\text{ J} \end{gathered}`

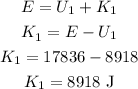
Thus, the kinetic energy at halfway is 8918 J.

(d). The potential energy at the bottom of the cliff is,

`\begin{gathered} U_2=mg(0) \\ U_2=0\text{ J} \end{gathered}`

Thus, the kinetic energy of the diver just before hitting the water is,

`\begin{gathered} K_2=E-U_2 \\ K_2=17836-0 \\ K_2=17836\text{ J} \end{gathered}`

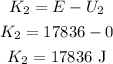
Thus, the kinetic energy of the diver just before hitting the water is 17836 J.