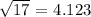Question

How do you find the square root of 17 without a calculator?

Answer 1

Step 1

`√(17)`

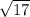
Step 2:

Write a perfect square number before 17 and after 17.

The numbers are: 16 and 25.

Step 3:

`\begin{gathered} \sqrt{16\text{ }}\text{ = 4} \\ √(17)\text{ = ?} \\ √(25)\text{ = 5} \end{gathered}`

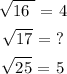
Step 4

The square root of 17 is a number less than 5 but greater than 4

`\begin{gathered} Decimal\text{ digit = 5 - 4 = 1} \\ √(17)\text{ = 4.1} \end{gathered}`

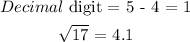
Find the square root of 17 by long division method

To find the square root of 17 by long division method we follow the steps given below

Start grouping the number in pairs from the right end. For 17, both the numbers will be grouped under one bar.

Determine the largest number, which, when multiplied with itself, will give 17 or a smaller number closest to 17. 4 is the required number.

Divide 17 by 4

We obtain the remainder as 1 in this step. Now, we will place 3 pairs of zeros after the decimal point and continue the long division. Get down one pair of zeros down. Add the quotient 4 to the divisor, which is also 4. Thus, 8 will be placed as the new divisor on the tens place, with a blank on one’s place.

Here, ( 81 × 1 = 81) is the closest to 100. So 1 will be placed on the blank place.

The remainder obtained of this step is 19. Now, bring down the second pair of zeros.

On repeating the above step, the quotient from the previous step, which is 1, will be added to the divisor from the previous step (81). 82 along with a blank on digit in ones will be the new divisor.

The above set is repeated and s 822 × 2 = 1644 is the closest to 1900.

The same procedure is followed and for the remainder of 256 by bringing down another pair of zeros down.

Next

Final answer

`√(17)\text{ = 4.123}`