To solve this we are going to use the angular momentum, to calculate de distance of the red spot. The momentum is not going to change, so the initial total momentum has to be the same as the final total momentum
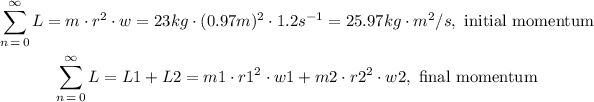
Both momentums are the same, so now we can equal both expressions
![\begin{gathered} m1\cdot r1^2\cdot w1+m2\cdot r2^2\cdot w2=25.97 \\ 23kg\cdot0.97^2\cdot(1-0.08)(1.2)+1.2kg\cdot r2^2\cdot(1-0.08)(1.2)=25.97,\text{ \lparen1-0.08\rparen is the reduction of 8\% in speed} \\ 23.89+1.32\cdot r2^2=25.97 \\ (2.08)/(1.32)=r2^2 \\ r2=1.25m \end{gathered}]()