Question

How would I answer this question by using this method:- finding E using E=KQ/r^2- plugging that value into 2Ecostheta to get the final answer

Answer 1

455555.6 N/C

Explanation:

We have that Coulomb's law allows us to calculate the electric field as follows

`\begin{gathered} E=k\cdot\frac{Q_{}}{r^2} \\ \text{where:} \\ k=9\cdot10^9N\cdot(m^2)/(C^2) \\ Q=41\cdot10^(-6)C \\ r=0.9\text{ m} \end{gathered}`

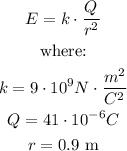
We have that the net electric field would be:

`\begin{gathered} E_{\text{net,y}}=0 \\ E_{\text{net,x}}=E_{\text{net}} \\ E_{\text{net}}=E_(l,x)+E_(r,x) \\ E_(l,x)=k\cdot\frac{Q_{}}{r^2} \\ E_(r,x)=k\cdot\frac{Q_{}}{r^2} \\ E_{\text{net}}=2\cdot(k\cdot\frac{Q_{}}{r^2})\cdot\cos \theta \end{gathered}`

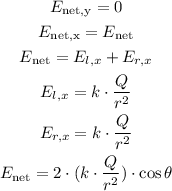
Being an equilateral triangle all its angles are equal, therefore it is equal to 60° (since the sum of all the angles in a triangle is equal to 180°, then 180°/3 = 60°)

`\begin{gathered} E_{\text{net}}=2\cdot(9.10^9(41\cdot10^(-6))/(0.9^2))\cdot\cos 60 \\ E_{\text{net}}=2\cdot(455555.55)\cdot\cos 60 \\ E_{\text{net}}=455555.6(N)/(C) \end{gathered}`

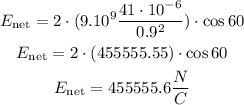
The electric field is 455555.6 N/C