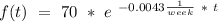Question

Find the exponential function that satisfies the given conditions: Initial value = 70, decreasing at a rate of 0.43% per week

Answer 1

`f(t) \ = \ 70 \ * \ e ^ { \ - 0.0043 (1)/(week) \ * \ t}`

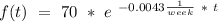
Explanation:

Exponentials functions are of the form:

`f(t) \ = \ A \ * \ e ^ { \ b \ * \ t}`

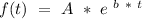
where A and b are constants.

Now, the initial value of the exponential function its

`f(0) \ = \ A \ * \ e ^ { \ b \ * \ 0}`

`f(0) \ = \ A \ * \ e ^ { \ 0 \ }`

`f(0) \ = \ A \`

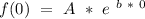
If the initial value must be 70, this must means:

`A \ = \ 70`

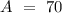
So

`f(t) \ = \ 70 \ * \ e ^ { \ b \ * \ t}`

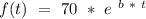
We also know that it must decrease at a rate of 0.43 %, this mean that after one week we got:

`100 \ \% - 0.43 \ \%  = 99.57 \ \%`

`f(1 week) \ = \ 70 \ * 0.9957 \ =  \ 70 \ * \ e ^ { \ b \ * \ 1 \ week}`

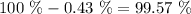
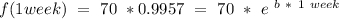
This means :

`0.9957 \ = \ e ^ { \ b \ * \ 1 \ week}`

`ln ( 0.9957) \ = \ b \ * \ 1 \ week`

`\ b \ = (ln ( 0.9957))/( 1 \ week)`

`\ b \ = - 0.0043 (1)/(week)`

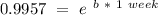
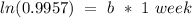
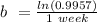
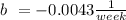
So, our equation, finally, its:

`f(t) \ = \ 70 \ * \ e ^ { \ - 0.0043 (1)/(week) \ * \ t}`

Answer 2

That'd be y = 70* (1-.00043)^t, where the rate of decrease is really 0.43% and t denotes the # of weeks.

This simplifies to y = 70*(0.00057)^t.