Question

A new surgery is successful 80% of the time. If the results of 6 such surgeries are randomly sampled, what is the probability that more than 3 of them are successful?Carry your intermediate computations to at least four decimal places, and round your answer to two decimal places.

Answer 1

In this problem, we have a binomial probability distribution

where

p=80%=0.80

q=1-p -----> q=0.20 probability of fail

the probability that more than 3 of them are successful is

P(X>3)=P(x=4)+P(X=5)+P(x=6)

step 1

Find out P(X=4)

`\begin{gathered} P(X=4)=(6!)/(4!(6-4)!)*0.80^4*0.20^2 \\ P(X=4)=0.24576 \end{gathered}`

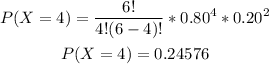
step 2

Find out P(X=5)

`\begin{gathered} P(X=5)=(6!)/(5!(6-5)!)*0.80^5*0.20^1 \\ P(X=5)=0.393216 \end{gathered}`

step 3

Find out P(X=6)

`\begin{gathered} P(X=6)=(6!)/(6!(6-6)!)*0.80^6*0.20^0 \\ P(X=6)=0.262144 \end{gathered}`

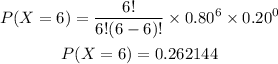
step 4

Adds the probabilities

P(X>3)=0.24576+0.393216+0.262144

P(X>3)=0.90112

therefore

The answer is 0.90