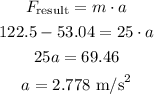Question

41. A 25 kg box is released on a 30 degree incline. Find the acceleration down the incline if the coefficient of friction is 0.25.

Answer 1

First, let's draw the free body diagram:

Let's decompose the weight force into two components, one parallel to the friction (Wx) and one parallel to the normal force (Wy):

`\begin{gathered} Wx=W\cdot\sin (\theta) \\ Wx=25\cdot9.8\cdot\sin (30\degree) \\ Wx=25\cdot9.8\cdot0.5 \\ Wx=122.5\text{ N} \\ \\ Wy=W\cdot\cos (\theta) \\ Wy=25\cdot9.8\cdot\cos (30\degree) \\ Wy=25\cdot9.8\cdot0.866 \\ Wy=212.17\text{ N} \end{gathered}`

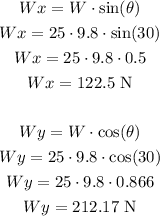
The normal force has the same magnitude as Wy, so let's calculate the friction force:

`\begin{gathered} F_f=N\cdot\mu \\ F_f=212.17\cdot0.25 \\ F_f=53.04\text{ N} \end{gathered}`

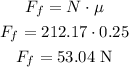
Since Wx is greater than the friction force, the box will move, and the acceleration is:

`\begin{gathered} F_{\text{result}}=m\cdot a \\ 122.5-53.04=25\cdot a \\ 25a=69.46 \\ a=2.778\text{ m/s}^2 \end{gathered}`