Question

Which point is a solution to the inequality shown in this graph?

Answer 1

ur answer is (0,-3)

because ur line is a solid line, this means any number on that line is a solution....along with any points that are in the blue area. when u plot ur answer choices, if it falls in the white area, it is not a solution

Answer 2

(0,-3) is the only solution to the inequality shown in this graph

Explanation:

Given : A graph with two points (5,0) and (0,-3).

we have to select which point is a solution to the inequality shown in graph given.

Consider the two given points on graph as (5,0) and (0,-3)

The standard equation of line is given by y = mx + c , where m is slope and c is y- intercept.

Slope between two points is given by

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(5,\:0\right),\:\left(x_2,\:y_2\right)=\left(0,\:-3\right)`

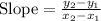
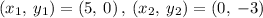
Thus, we get,

`m=(3)/(5)`

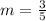
Also, given y- intercept is -3

so, equation of line is
`y=(3)/(5)x-3`

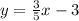
Now, for the region, let test point be (0,0)

Put in equation of line

`0\geq(3)/(5)0-3`

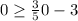
Thus, The inequality shown in graph is
`y\geq(3)/(5)x-3`

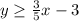
Now , we check each given point for the given inequality , by plotting it on th graph.

Those point that lies in the shaded region or on the boundary will be the solution of the given graph

Thus, only (0, -3) lies in the area of shaded portion.

Thus, (0,-3) is the only solution to the inequality shown in this graph