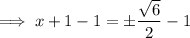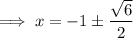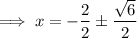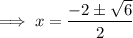Answer:
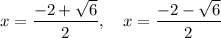
Explanation:
Given quadratic equation:
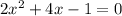
Solve by completing the square
Move the constant to the right side of the equation:
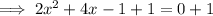
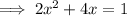
Factor out the common factor of 2 from the left side:
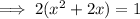
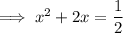
Add the square of half the coefficient of the term in x to both sides of the equation:
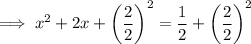
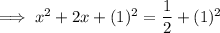
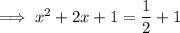
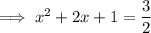
Factor the perfect square trinomial on the left side of the equation:
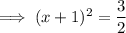
Square root both sides:
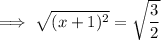
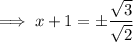
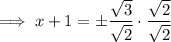
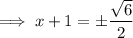
Subtract one from both sides: