Question

For ΔABC, ∠A = 3x - 8, ∠B = 5x - 6, and ∠C = 4x + 2. If ΔABC undergoes a dilation by a scale factor of 1 2 to create ΔA'B'C' with ∠A' = 2x + 8, ∠B' = 90 - x, and ∠C' = 5x - 14, which confirms that ΔABC∼ΔA'B'C by the AA criterion?

Answer 1

We all know that a triangle has 180 degrees.
3x-8+5x-6+4x+2=180
12x-12=180
12x=180+12
12x=192
x=16.


∠A=2(16)+8=40
∠B= 90-16=74
∠C = 5(16) -14= 66

Answer 2

`\triangle ABC \sim \triangle A'B'C'`

Explanation:

We are given the following information in the question:

`\triangle ABC \sim \triangle A'B'C'`

`\angle A = 3x - 8, \angle B = 5x - 6, \angle C = 4x + 2.`

`\angle A' = 2x + 8, \angle B' = 90 - x,  \angle C' = 5x - 14`

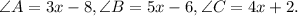
According to angle sum property of triangle the sum of all the three angles of triangle is 180.

`\triangle ABC\\\angle A + \angle B + \angle C = 180^\circ\\3x -8+5x-6+4x+2 = 180\\12x-12 = 180\\12x = 192\\x = 16`

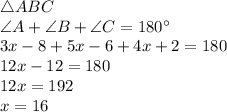
For the two triangles to be similar by AA criterion.

`\angle A = \angle A'\\\angle B = \angle B'`

`\angle A = 3x - 8 = 40\\\angle A' = 2x + 8 = 40\\\angle B = 5x - 6 = 74\\\angle B' = 90 - x = 74`

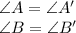
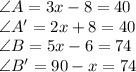
Thus, this confirms that the triangles are congruent.

`\triangle ABC \sim \triangle A'B'C'`