Question

An asteroid follows a hyperbolic path defined by the equation 16x2 − 9y2 = 576. If one of its foci is the sun’s position, the minimum distance between the asteroid and the sun is

Answer 1

I could give you some works
Here is for you!

Answer 2

The minimum distance between the asteroid and the sun is 10 - 6 =4

Explanation:

The given hyperbolic path defined as
`16x^(2)-9y^(2)=576`

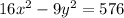
divide both the sides by 576,

`(16x^(2))/(576)-(9y^(2))/(576)=(576)/(576)`

`(x^(2))/(36)-(y^(2))/(64)=1`

`(x^(2))/(36)-(y^(2))/(64)=1`

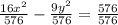
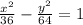
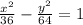
The general equation of hyperbola is written as

;

`(x^(2))/(a^(2))-(y^(2))/(b^(2))=1`

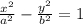
Compare
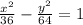`(x^(2))/(36)-(y^(2))/(64)=1` with above mention equation

Here
`a^(2)=36 \ \text{and} \ b^(2)=64`

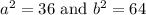
The distance between the asteroid and the sun is seen by figure -1

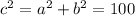`c^(2)=a^(2)+b^(2)=100` or
`c^(2)=100`

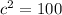
⇒c =10

The minimum distance between the asteroid and the sun is 10 -6 =4