Question

(Score for Question 1: of 10 points)1. Consider the quadratic function.(d) Graph the function on the coordinate plane. Include the axis of symme(b) What is the equation of the axis of symmetry?(c) What are the coordinates of the vertex?(a) What are the x-intercepts and y-intercept?Answer:f(x) = - (x + 4) * (x - 1)

Answer 1

Given:

`f(x)=-(x+4)(x-1)`

Step-by-step explanation:

a) To draw: The Graph

Let us find the intercepts.

When x = 0, we get

`\begin{gathered} y=-(4)(-1) \\ y=4 \end{gathered}`

Therefore, the y-intercept is (0, 4).

The x-intercepts are,

`(-4,0),(1,0)`

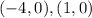
Let us find the vertex.

The given function can be written as,

`\begin{gathered} f(x)=-(x+4)(x-1) \\ =-(x^2+3x-4) \\ =-(x^2+3x+((3)/(2))^2-((3)/(2))^2-4) \\ =-[(x+(3)/(2))^2-(9)/(4)-4] \\ =-[(x+(3)/(2))^2-(25)/(4)] \\ f(x)=(x+(3)/(2))^2+(25)/(4) \end{gathered}`

So, the vertex is,

`\begin{gathered} (h,k)=(-(3)/(2),(25)/(4)) \\ (or) \\ (h,k)=(-1.5,6.25) \end{gathered}`

The graph becomes,

b) The equation of symmetry is,

`x=-(3)/(2)`

This line divides the parabola into two equal parts.

c) The coordinates of the vertex is,

`(h,k)=(-1.5,6.25)`

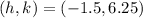
d) Intercepts:

The x-intercepts are,

`(-4,0),(1,0)`

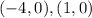
The y-intercept is (0, 4).