Question

The first four terms of a geometric sequence are 108, 36, 12, 4, … What is the common ratio?

–72
–3
3
1/3

Answer 1

The first four terms of a geometric sequence are 108, 36, 12, 4, … What is the common ratio?
–72
–3
3
☆☆☆☆☆☆☆☆1/3

Answer 2

Option 4th is correct

`(1)/(3)`

Explanation:

Common ratio(r) defined as the ratio of a term to the previous term.

`r = (a_2)/(a_1) = (a_3)/(a_2)......................(a_(n+1))/(a_n)`

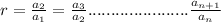
As per the statement:

The first four terms of a geometric sequence are

108, 36, 12, 4, …

Here,

`a_1 = 108`

`a_2 = 36`

`a_3 = 12`

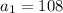
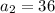
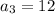
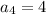`a_4 = 4` and so on...

We have to find the common ratio.

By definition we have;

`r= (1)/(3)`

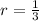
Since;

`r = (36)/(108) =(12)/(36)=(4)/(12).........=(1)/(3)`

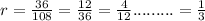
Therefore, the common ratio is,
`(1)/(3)`