Question

A newspaper article reported that people spend a mean of 7.5 hours per day watching TV, with a standard deviation of 2.0 hours. A psychologist would like to conduct interviews with the 20% of the population who spend the most time watching TV. She assumes that the daily time people spend watching TV is normally distributed. At least how many hours of daily TV watching are necessary for a person to be eligible for the interview? Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place.

Answer 1

Given:

Mean = 7.5 hours

Standard deviation = 2.0 hours

Interview 20% of the population

Let x = daily time people spend watching TV.

Therefore, The z score probability distribution for normal distribution is given by:

`z=(x-\mu)/(\sigma)`

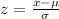
Where:

μ = mean = 7.5 hours

σ = standard deviation = 2.0 hours

Using the table of the critical value we find the z value for the top 20%.

`z(0.20)=0.8416`

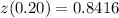
Next, substitute the given values in the formula of z:

`0.8416=(x-7.5)/(2.0)`

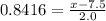
And solve for x:

`\begin{gathered} 2.0*0.8416=2.0*(x-7.5)/(2.0) \\ 1.6832=x-7.5 \\ 1.6832+7.5=x-7.5+7.5 \\ 9.1832=x \end{gathered}`

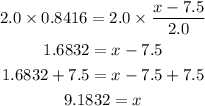
Therefore, at least 9.2 hours of daily TV watching is necessary for a person to be eligible for the interview.

Answer: 9.2 hours per day