Question

Can you please help me

Answer 1

The diagram shows an image of intersecting secants. We would use the intersecting secants theorem in the image below to solve the question.

We compare the image above with the diagram in the question

This implies that the solution would be

`\begin{gathered} AE* AD=AB* AC \\ \end{gathered}`

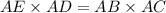
AE=21+9=30

AD=9

AB=10

AC=10+x

Substituting the parameters in the secant theorem above, we then have;

`\begin{gathered} 30*9=10*(10+x) \\ 270=100+10x \\ 10x=270-100 \\ 10x=170 \\ x=(170)/(10) \\ x=17 \\ \end{gathered}`

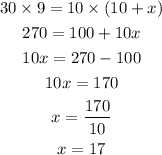
Therefore, the length of x is 17