Question

The equation mx2 + 12x + 9m = 0 has different roots for different values of m. For what values of m will the equation have one repeated root?

Answer 1

b^2 - 4ac = 0
12^2 - 4m(9m) = 0
144 = 36m^2
m^2 = 4
m = ± 2
Hope This Helps!
-TyyBenjii

Answer 2

The value of m would be 2 or - 2.

Explanation:

Since, a quadratic equation
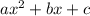`ax^2+bx+c` has two different real roots,

If
`b^2-4ac> 0`

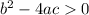
It has two equal real roots,

If
`b^2-4ac=0`

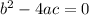
While it has two different complex roots,

If
`b^2-4ac<0`

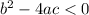
Here, the given equation is,

`mx^2+12x+9m=0`

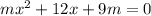
By comparing,

a = m, b = 12 and c = 9m,

By the above properties,

For equal roots,

`(12)^2-4(m)(9m)=0`

`144-36m^2=0`

`-36m^2 = -144`

`m^2 = 4\implies m\pm 2`

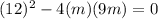
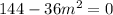
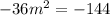
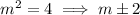
Hence, the value of m would be 2 or - 2.