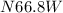SOLUTION
Let us represent this using a diagram
From the diagram above, h represents the Fisherman's distance back to the marina.
Now we can see that a right-angle triangle has been made. So to find h, which represents the hypotenuse of the right-angle above, we use Pytagoras theorem. we have
![\begin{gathered} \text{hyp}^2=opp^2+adj^2 \\ h^2=3^2+7^2 \\ h^2=9+49 \\ h^2=58 \\ h=\sqrt[]{58} \\ h=7.615773 \\ h=7.6\text{ miles } \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xhifutmgzpyymqhtm5u8.png)
Hence his distance from the marina is 7.6 miles to the nearest tenth.
To find his direction, let us find the acute angle
From SOHCAHTOA, we have that
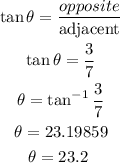
So, from the diagram, his bearing is 90 degree + the angle theta. So we have
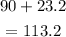
So his distance is 7.6 miles on a bearing of 113.2 degrees
You can also subtract 23.2 from 90 degree to get his direction in north-west, we have
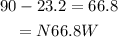
So we can say his distance is 7.6 miles on a bearing of