Question

Solve for the roots in the following equation. Hint: Factor both quadratic expressions.

(x 4 + 5x 2 - 36)(2x 2 + 9x - 5) = 0

Answer 1

Solve for x:
(13 x - 5) (14 x - 36) = 0
Split into two equations:
13 x - 5 = 0 or 14 x - 36 = 0
Add 5 to both sides:
13 x = 5 or 14 x - 36 = 0
Divide both sides by 13:
x = 5/13 or 14 x - 36 = 0
Factor constant terms from the left hand side:
x = 5/13 or 2 (7 x - 18) = 0
Divide both sides by 2:
x = 5/13 or 7 x - 18 = 0
Add 18 to both sides:
x = 5/13 or 7 x = 18
Divide both sides by 7:
Answer: x = 5/13 or x = 18/7

Answer 2

2, -2, 3, -3, -5 and 1/2.

Explanation:

We have the product
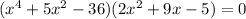`(x^4 + 5x^2 - 36)(2x^2 + 9x - 5) = 0`. As we have a product equal to 0, one of the factors (or both) need to be 0. Then,

`(x^4 + 5x^2 - 36)= 0` or
`(2x^2 + 9x - 5) = 0`.

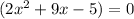For the left expression:

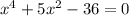`x^4 + 5x^2 - 36= 0`, we are going to apply synthetic division (the process is in the picture below) and obtain that the factorization is:

`x^4 + 5x^2 - 36= (x-2)(x^3+2x^2+9x+18)=0.`

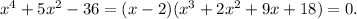
For the grade three expression we apply the same process and obtain:

`(x-2)(x^3+2x^2+9x+18)=(x-2)(x-(-2))(x^2-9)=0.`

Finally, the grade two expression can be factored with difference of squares:

`(x-2)(x+2)(x^2-9)=(x-2)(x+2)(x-3)(x+3)=0.`

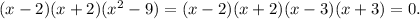
Then, the roots are 2, -2, 3 and -3.

For the right expression:

`2x^2 + 9x - 5=0`

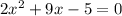
We can apply the case of factorization with the form
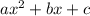`ax^2+bx+c`. First we multiply and divide the expression by the coefficient of x^2, that is by 2:

`(4x^2 + 9(2x) - 10)/(2)`

Then, we factor the numerator (2x+a)(2x+b) by searching two numbers that multiplied are -10 and added are 9, those are 10 and -1:

`((2x+10)(2x-1))/(2)`

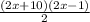
Finally, we divide by 2 the factor with even coefficients, if the expression hasn't even expressions stay it:

`(x+5)(2x-1)`

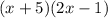
Then, the roots are

x+5 = 0, x=-5 and

2x-1 = 0

2x = 1.

x = 1/2.

We have finally 6 roots in total: 2, -2, 3, -3, -5 and 1/2.